set là gì? Bạn đang tìm hiểu về khái niệm tập hợp trong toán học hay cấu trúc dữ liệu set trong lập trình? Dù mục đích của bạn là gì, bài viết này của KTH GARDEN sẽ giúp bạn hiểu rõ định nghĩa set, khám phá ứng dụng của set trong nhiều lĩnh vực, từ toán học rời rạc đến lập trình hướng đối tượng.
Chúng ta sẽ cùng nhau tìm hiểu khái niệm set một cách đơn giản, dễ hiểu, đi sâu vào các khái niệm như phần tử tập hợp, tập hợp con, hợp của tập hợp, giao của tập hợp và hiệu của tập hợp. Bài viết sẽ cung cấp nhiều ví dụ về set minh họa và hướng dẫn cách sử dụng set trong các ngôn ngữ lập trình phổ biến như Python và Java. Chuẩn bị sẵn sàng khám phá thế giới thú vị của tập hợp cùng KTH GARDEN nhé!
Định nghĩa “Set” (Tập hợp) trong Toán học và Lập trình
Set, hay còn gọi là tập hợp, là một khái niệm nền tảng trong cả toán học và lập trình. Trong toán học, set được định nghĩa là một bộ sưu tập các phần tử riêng biệt, không cần thiết phải theo một thứ tự cụ thể. Những phần tử này có thể là bất cứ thứ gì: số, chữ cái, các đối tượng khác, thậm chí là các tập hợp khác. Ví dụ, {1, 2, 3} là một tập hợp gồm ba số nguyên dương. Khác với mảng (array) trong lập trình, tập hợp không có thứ tự, và mỗi phần tử chỉ xuất hiện một lần. Điều này có nghĩa là {1, 2, 2, 3} thực chất sẽ được xem là {1, 2, 3}.
Một trong những đặc điểm quan trọng của tập hợp là tính chất thuộc hay không thuộc. Một phần tử có thể thuộc về một hoặc nhiều tập hợp, hoặc không thuộc bất kỳ tập hợp nào. Ví dụ, phần tử ‘a’ thuộc tập hợp {a, b, c}, nhưng không thuộc tập hợp {1, 2, 3}. Tập hợp rỗng, ký hiệu là ∅ hoặc {}, là một tập hợp không chứa bất kỳ phần tử nào. Đây là một khái niệm quan trọng trong lý thuyết tập hợp và được sử dụng rộng rãi trong các chứng minh toán học. Có nhiều loại tập hợp khác nhau, chẳng hạn như tập hợp hữu hạn (chứa một số lượng phần tử hữu hạn, ví dụ: tập hợp các số tự nhiên từ 1 đến 10) và tập hợp vô hạn (chứa một số lượng phần tử vô hạn, ví dụ: tập hợp tất cả các số tự nhiên). Việc phân loại tập hợp này giúp chúng ta phân tích và nghiên cứu các tính chất của chúng một cách hiệu quả hơn.
Phép toán trên tập hợp cũng là một phần quan trọng trong toán học, bao gồm các phép toán cơ bản như: hợp (union), giao (intersection), hiệu (difference). Hợp của hai tập hợp A và B, ký hiệu là A ∪ B, là một tập hợp chứa tất cả các phần tử thuộc A hoặc B hoặc cả hai. Giao của hai tập hợp A và B, ký hiệu là A ∩ B, là một tập hợp chỉ chứa các phần tử thuộc cả A và B. Hiệu của hai tập hợp A và B, ký hiệu là A B, là tập hợp chứa các phần tử thuộc A nhưng không thuộc B. Các phép toán này là cơ sở để xây dựng các cấu trúc toán học phức tạp hơn. Hiểu rõ các phép toán này giúp bạn giải quyết các bài toán liên quan đến tập hợp một cách dễ dàng hơn. Ví dụ, nếu A = {1, 2, 3} và B = {3, 4, 5}, thì A ∪ B = {1, 2, 3, 4, 5}, A ∩ B = {3}, và A B = {1, 2}.
Set trong Toán học: Khái niệm, các loại tập hợp và phép toán trên tập hợp
Như đã đề cập ở trên, set trong toán học là một khái niệm cơ bản và quan trọng. Nắm vững khái niệm này là tiền đề để hiểu được nhiều lĩnh vực toán học khác, đặc biệt là toán học rời rạc và lý thuyết tập hợp. Một trong những cách để biểu diễn tập hợp là sử dụng biểu đồ Venn, một công cụ trực quan giúp minh họa các quan hệ giữa các tập hợp. Biểu đồ Venn sử dụng các hình tròn để biểu diễn các tập hợp, và các vùng chồng chéo giữa các hình tròn thể hiện giao của các tập hợp đó. Ví dụ, để minh họa cho phép hợp, vùng phủ hết các hình tròn sẽ biểu diễn tập hợp hợp.
Ngoài các phép toán cơ bản, còn có nhiều phép toán khác trên tập hợp như tích Descartes, lũy thừa tập hợp, v.v… Tích Descartes của hai tập hợp A và B là tập hợp tất cả các cặp có thứ tự (a, b) sao cho a thuộc A và b thuộc B. Lũy thừa tập hợp của A là tập hợp tất cả các tập con của A. Những phép toán này có ứng dụng rộng rãi trong nhiều lĩnh vực toán học khác nhau.
Ngoài tập hợp hữu hạn và vô hạn, ta còn có các loại tập hợp khác như tập hợp đếm được (có thể lập ra một song ánh giữa tập hợp đó và tập hợp các số tự nhiên) và tập hợp không đếm được (không thể lập ra một song ánh giữa tập hợp đó và tập hợp các số tự nhiên). Một ví dụ kinh điển của tập hợp không đếm được là tập hợp tất cả các số thực trong khoảng [0, 1]. Sự tồn tại của các tập hợp không đếm được chứng tỏ rằng “vô hạn” cũng có nhiều mức độ khác nhau. Thậm chí có những tập hợp vô hạn lớn hơn tập hợp các số tự nhiên vô hạn đếm được.
Một khái niệm quan trọng khác liên quan đến tập hợp là quan hệ giữa các tập hợp, bao gồm quan hệ tập con (subset), tập con thực sự (proper subset). Tập hợp A là tập con của tập hợp B nếu mọi phần tử của A đều là phần tử của B. A là tập con thực sự của B nếu A là tập con của B và A khác B. Việc hiểu rõ các quan hệ này rất quan trọng trong việc phân tích và so sánh các tập hợp.
Set trong Lập trình: Ứng dụng và Cấu trúc Dữ liệu Set
Trong lập trình, set là một cấu trúc dữ liệu được sử dụng để lưu trữ một tập hợp các phần tử duy nhất. Khác với danh sách (list) hoặc mảng (array) cho phép phần tử trùng lặp, set chỉ lưu trữ mỗi phần tử một lần. Điều này rất hữu ích trong việc loại bỏ các phần tử trùng lặp và kiểm tra xem một phần tử có tồn tại trong tập hợp hay không. Tốc độ tìm kiếm trong set thường nhanh hơn so với danh sách vì set thường được cài đặt dựa trên cấu trúc dữ liệu như cây tìm kiếm nhị phân hoặc bảng băm. Nhờ đó, việc kiểm tra xem một phần tử có thuộc về set hay không có độ phức tạp thời gian trung bình là O(1), trong khi với danh sách là O(n).
Các ngôn ngữ lập trình hiện đại như Python, Java, C++, JavaScript đều hỗ trợ cấu trúc dữ liệu set. Trong Python, set được khai báo bằng cách sử dụng cặp ngoặc nhọn {} hoặc hàm set(). Ví dụ: my_set = {1, 2, 3}. Trong Java, set được triển khai thông qua các interface như Set, HashSet, TreeSet, mỗi loại có đặc điểm và hiệu suất khác nhau. HashSet có tốc độ truy cập nhanh hơn nhưng không đảm bảo thứ tự các phần tử, trong khi TreeSet đảm bảo thứ tự nhưng tốc độ truy cập chậm hơn một chút. Sự lựa chọn phụ thuộc vào nhu cầu cụ thể của ứng dụng.
Set được sử dụng rộng rãi trong nhiều ứng dụng lập trình khác nhau. Ví dụ: loại bỏ các phần tử trùng lặp trong một danh sách, kiểm tra xem một phần tử có tồn tại trong một tập hợp hay không, thực hiện các phép toán tập hợp như hợp, giao, hiệu. Trong xử lý ngôn ngữ tự nhiên, set được sử dụng để lưu trữ từ vựng của một văn bản. Trong đồ họa máy tính, set được sử dụng để biểu diễn các tập hợp điểm hoặc hình ảnh. Với tính năng lưu trữ các phần tử duy nhất và khả năng thực hiện các phép toán tập hợp hiệu quả, set đóng vai trò quan trọng trong việc tối ưu hóa hiệu năng của chương trình. Một ví dụ khác là sử dụng set để kiểm tra xem hai chuỗi có chứa cùng một tập hợp các ký tự hay không, giúp tối ưu hóa việc so sánh trong một số thuật toán. Đặc biệt, với các ứng dụng cần kiểm tra sự tồn tại của phần tử một cách nhanh chóng thì set là lựa chọn tối ưu.
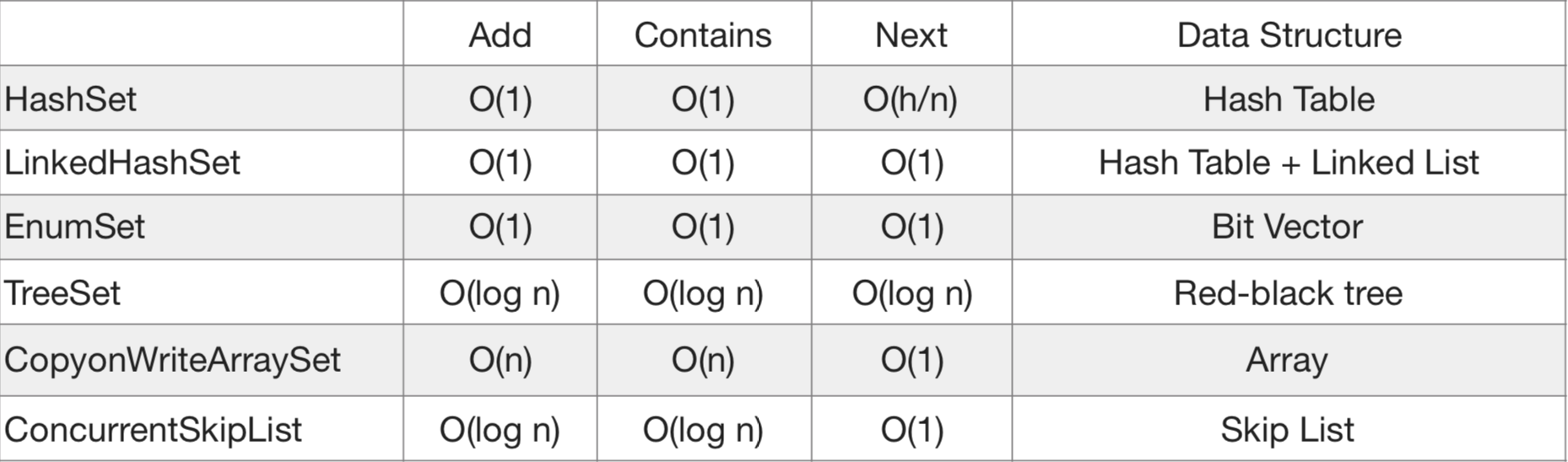
So sánh Set với các Cấu trúc Dữ liệu khác trong Lập trình
Set, hay tập hợp, là một cấu trúc dữ liệu quan trọng trong lập trình, nhưng nó không phải là lựa chọn duy nhất. Việc lựa chọn cấu trúc dữ liệu phù hợp phụ thuộc rất nhiều vào mục đích sử dụng và đặc điểm của dữ liệu. Hãy cùng so sánh set với một số cấu trúc dữ liệu khác thường được sử dụng để thấy rõ điểm mạnh, điểm yếu và trường hợp áp dụng của mỗi loại.
Một trong những cấu trúc dữ liệu thường được so sánh với set là mảng (array). Mảng cho phép lưu trữ các phần tử có thứ tự, truy cập nhanh chóng bằng chỉ số. Tuy nhiên, mảng không đảm bảo tính duy nhất của phần tử, và việc tìm kiếm, xóa một phần tử trong mảng lớn có thể rất tốn kém về thời gian, đặc biệt là với các mảng không được sắp xếp. Ngược lại, set ưu tiên tính duy nhất của phần tử, và các thao tác như kiểm tra sự tồn tại của một phần tử, thêm hoặc xóa phần tử đều có độ phức tạp thời gian trung bình là O(1), nhanh hơn nhiều so với mảng trong hầu hết trường hợp. Tuy nhiên, mảng cho phép truy cập ngẫu nhiên tới các phần tử dựa trên chỉ số, trong khi set không hỗ trợ điều này. Ví dụ, nếu bạn cần truy cập phần tử thứ 5 trong một danh sách, mảng sẽ hiệu quả hơn set.
Tiếp theo, hãy so sánh set với danh sách (list). Danh sách, tương tự như mảng, cho phép lưu trữ các phần tử có thứ tự và cho phép phần tử trùng lặp. Việc thêm phần tử vào đầu hoặc cuối danh sách tương đối nhanh chóng, nhưng việc tìm kiếm hoặc xóa một phần tử cụ thể có thể chậm hơn so với set, đặc biệt đối với danh sách lớn. Set lại nổi bật với khả năng đảm bảo tính duy nhất của phần tử và tốc độ nhanh chóng trong việc kiểm tra sự tồn tại của một phần tử. Nếu bạn cần một cấu trúc dữ liệu cho phép phần tử trùng lặp và thứ tự quan trọng, danh sách là lựa chọn tốt hơn; nếu tính duy nhất và tốc độ truy vấn là ưu tiên hàng đầu, set là lựa chọn phù hợp hơn. Một ví dụ thực tế là, nếu bạn cần lưu trữ danh sách sinh viên trong một lớp học, nơi mà sinh viên có thể trùng tên, list là phù hợp. Tuy nhiên, nếu bạn cần lưu trữ danh sách các mã sinh viên duy nhất, set sẽ là lựa chọn tốt hơn.
Set cũng thường được so sánh với từ điển (dictionary) hoặc bảng băm (hash table). Từ điển lưu trữ dữ liệu dưới dạng cặp khóa-giá trị, cho phép truy cập nhanh chóng dựa trên khóa. Nếu bạn cần tìm kiếm một phần tử dựa trên một thuộc tính cụ thể, từ điển sẽ hiệu quả hơn set. Ví dụ, nếu bạn có một tập hợp sinh viên với mã sinh viên và tên, bạn có thể sử dụng từ điển để tìm kiếm sinh viên dựa trên mã sinh viên của họ. Tuy nhiên, nếu bạn chỉ cần biết liệu một sinh viên có trong tập hợp hay không, không cần thông tin khác, set sẽ đơn giản và hiệu quả hơn.
Ngoài ra, tùy thuộc vào ngôn ngữ lập trình, set có thể có các đặc điểm khác biệt. Ví dụ, trong Python, set là một cấu trúc dữ liệu không thể thay đổi (immutable) sau khi được tạo, còn trong Java, việc thay đổi set là hoàn toàn có thể. Điều này cũng cần được xem xét khi lựa chọn giữa các cấu trúc dữ liệu. Thậm chí, một số ngôn ngữ lập trình cung cấp các loại set chuyên biệt với các chức năng bổ sung, tối ưu cho các trường hợp sử dụng cụ thể.
Tóm lại, lựa chọn giữa set và các cấu trúc dữ liệu khác phụ thuộc vào yêu cầu cụ thể của ứng dụng. Nếu bạn cần một cấu trúc dữ liệu đảm bảo tính duy nhất của phần tử, cho phép các thao tác như thêm, xóa, kiểm tra sự tồn tại nhanh chóng, và không yêu cầu thứ tự hay truy cập ngẫu nhiên, thì set là một lựa chọn tuyệt vời. Nhưng nếu yêu cầu của bạn khác đi, chẳng hạn cần lưu trữ thứ tự phần tử hoặc cho phép phần tử trùng lặp, thì các cấu trúc dữ liệu khác như mảng, danh sách hoặc từ điển có thể phù hợp hơn. Hiểu rõ điểm mạnh và điểm yếu của mỗi cấu trúc dữ liệu sẽ giúp bạn lựa chọn tối ưu cho từng trường hợp.
Ví dụ minh họa về Set trong Toán học và Lập trình
Để làm rõ hơn khái niệm set, chúng ta sẽ xem xét một số ví dụ cụ thể trong cả toán học và lập trình.
Trong toán học, một set là một tập hợp các phần tử phân biệt. Ví dụ: Set A = {1, 2, 3} là một set chứa ba phần tử số nguyên: 1, 2, và 3. Thứ tự các phần tử trong set không quan trọng, vì vậy Set A = {3, 1, 2} vẫn là cùng một set. Một set khác, Set B = {1, 2, 2, 3} sẽ được coi là Set {1, 2, 3} vì các phần tử trùng lặp sẽ được tự động loại bỏ. Một set có thể chứa các phần tử thuộc các loại khác nhau, ví dụ: Set C = {1, “hello”, 3.14}. Một set đặc biệt là set rỗng, ký hiệu là ∅ hoặc {}, không chứa bất kỳ phần tử nào.
Các phép toán trên set bao gồm hợp (union), giao (intersection), và hiệu (difference). Hợp của hai set A và B (ký hiệu A ∪ B) là một set mới chứa tất cả các phần tử thuộc A hoặc B hoặc cả hai. Giao của hai set A và B (ký hiệu A ∩ B) là một set mới chỉ chứa các phần tử thuộc cả A và B. Hiệu của hai set A và B (ký hiệu A B) là một set mới chứa các phần tử thuộc A nhưng không thuộc B. Ví dụ, nếu A = {1, 2, 3} và B = {3, 4, 5}, thì A ∪ B = {1, 2, 3, 4, 5}, A ∩ B = {3}, và A B = {1, 2}. Một thuộc tính ít được biết đến của tập hợp là khả năng kiểm tra xem một phần tử có thuộc tập hợp hay không.
Trong lập trình, việc sử dụng set rất linh hoạt. Hãy xem ví dụ trong Python:
my_set = {1, 2, 3}
print(my_set) # Output: {1, 2, 3}
my_set.add(4)
print(my_set) # Output: {1, 2, 3, 4}
my_set.remove(2)
print(my_set) # Output: {1, 3, 4}
print(1 in my_set) # Output: True
print(2 in my_set) # Output: False
Mã Python trên minh họa cách tạo một set, thêm phần tử, xóa phần tử, và kiểm tra sự tồn tại của một phần tử trong set. Các ngôn ngữ lập trình khác như Java, C++, C# cũng cung cấp cấu trúc dữ liệu set với các chức năng tương tự. Trong Java, bạn có thể dùng HashSet, TreeSet… mỗi loại có ưu điểm riêng biệt về hiệu suất, tùy vào cách bạn sử dụng, ví dụ TreeSet sẽ tự động sắp xếp các phần tử.
Một ví dụ khác trong thực tiễn: Giả sử bạn đang xây dựng một ứng dụng quản lý người dùng. Để đảm bảo mỗi người dùng chỉ có một tài khoản duy nhất, bạn có thể sử dụng một set để lưu trữ danh sách các tên người dùng. Khi một người dùng mới đăng ký, bạn chỉ cần kiểm tra xem tên người dùng đó đã có trong set hay chưa. Nếu chưa có, bạn mới cho phép người dùng đăng ký. Việc sử dụng set ở đây giúp đảm bảo tính toàn vẹn dữ liệu và hiệu suất của ứng dụng. Đây chỉ là một trong rất nhiều ứng dụng thực tiễn của set trong lập trình.
Các phép toán cơ bản trên tập hợp: Hợp, Giao, Hiệu
Các phép toán cơ bản trên set – hợp, giao, và hiệu – là những công cụ mạnh mẽ giúp thao tác và phân tích dữ liệu một cách hiệu quả. Hiểu rõ cách hoạt động của chúng là then chốt để sử dụng set một cách thành thục.
Hợp (Union): Phép hợp của hai set A và B, ký hiệu là A ∪ B, tạo ra một set mới chứa tất cả các phần tử có mặt trong ít nhất một trong hai set ban đầu. Các phần tử trùng lặp chỉ được tính một lần. Ví dụ, nếu A = {1, 2, 3} và B = {3, 4, 5}, thì A ∪ B = {1, 2, 3, 4, 5}. Trong lập trình, nhiều ngôn ngữ hỗ trợ phép toán hợp một cách trực tiếp thông qua các hàm hoặc toán tử. Ví dụ, trong Python, bạn có thể sử dụng toán tử | hoặc hàm union() để thực hiện phép hợp.
Giao (Intersection): Phép giao của hai set A và B, ký hiệu là A ∩ B, tạo ra một set mới chỉ chứa các phần tử có mặt trong cả hai set ban đầu. Ví dụ, nếu A = {1, 2, 3} và B = {3, 4, 5}, thì A ∩ B = {3}. Trong Python, toán tử & hoặc hàm intersection() có thể được sử dụng để tìm giao của hai set. Tốc độ của phép giao thường nhanh hơn so với việc thực hiện kiểm tra sự tồn tại của từng phần tử một cách thủ công, đặc biệt là khi xử lý các set lớn.
Hiệu (Difference): Phép hiệu của hai set A và B, ký hiệu là A B, tạo ra một set mới chứa tất cả các phần tử có mặt trong set A nhưng không có mặt trong set B. Ví dụ, nếu A = {1, 2, 3} và B = {3, 4, 5}, thì A B = {1, 2}. Ngược lại, B A = {4, 5}. Trong Python, toán tử – hoặc hàm difference() được sử dụng để thực hiện phép hiệu. Đây là một phép toán hữu ích khi bạn cần tìm các phần tử duy nhất trong một set so với một set khác. Ứng dụng thực tiễn của phép hiệu có thể là tìm ra những người dùng đã đăng ký dịch vụ A nhưng chưa đăng ký dịch vụ B.
Ngoài ba phép toán cơ bản này, còn có các phép toán khác như phép bù (complement), phép tích Descartes (Cartesian product),… tùy thuộc vào ngữ cảnh toán học hoặc ngôn ngữ lập trình cụ thể, nhưng hợp, giao và hiệu là những phép toán được sử dụng thường xuyên nhất. Việc hiểu rõ và áp dụng thành thục các phép toán này sẽ giúp bạn giải quyết nhiều bài toán phức tạp liên quan đến set một cách hiệu quả. Hãy nhớ rằng việc lựa chọn giữa việc sử dụng các hàm tích hợp sẵn và triển khai thủ công các phép toán này phụ thuộc vào yêu cầu về hiệu suất và khả năng đọc của mã nguồn. Trong nhiều trường hợp, việc sử dụng các hàm tích hợp sẵn sẽ đơn giản hơn và hiệu quả hơn.
